This is a brief dip into velocity distribution. It is not intended to be cited nor be academically through. Rather it will hopefully provide some insight and give you links to use other than Wikipedia.
Velocity Space
Imagine a container of particles. Gas particles. As these particles are whizzing about we notice this cloud of molecules seems to be equally spread out in all directions.
This is for several reasons:
- Brownian motion (random movement)
- Molecules prefer to be at equilibrium for the whole system
- They don’t want to be moving in the same direction
If we were to examine the velocities of the particles using velocity space, a 3D system
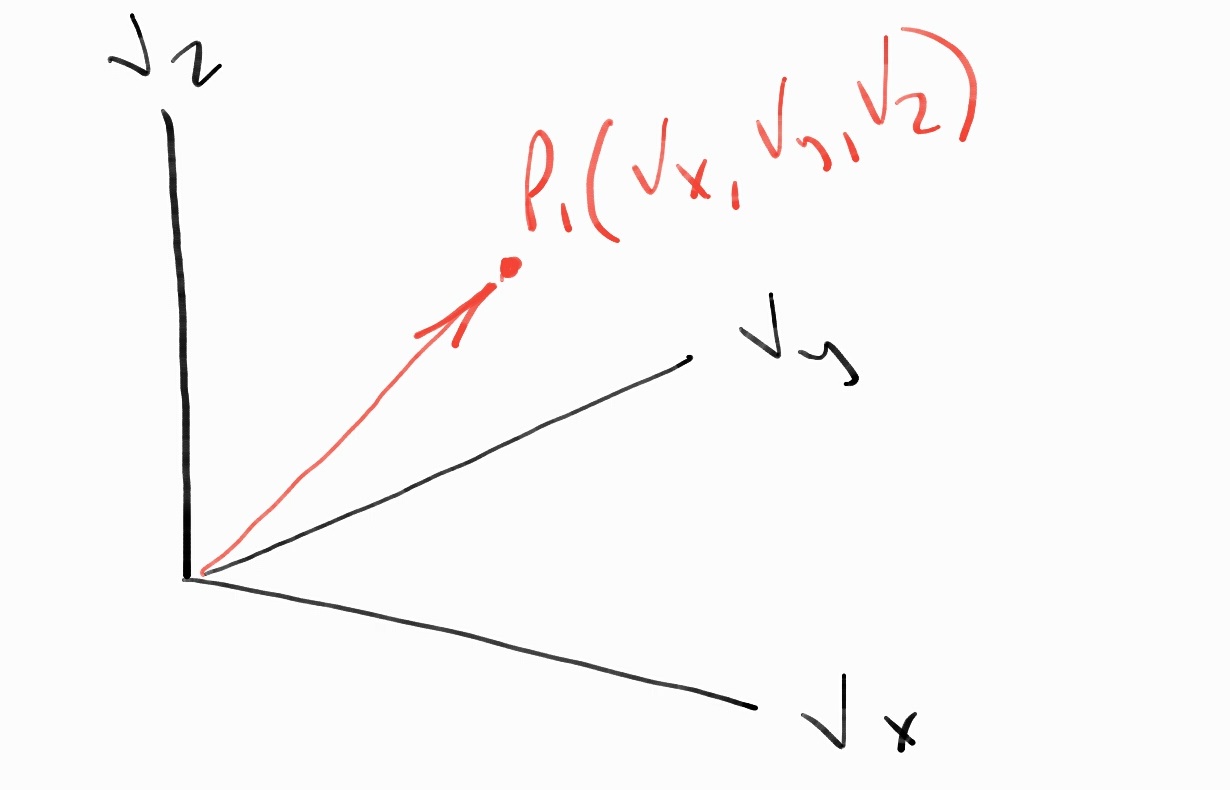
Velocity Space System
describing a particle’s velocity, we would find that they are evenly distributed as well.
We can imagine this as a shell. The velocities of all the particles will be distributed in a common range in order to achieve equilibrium.
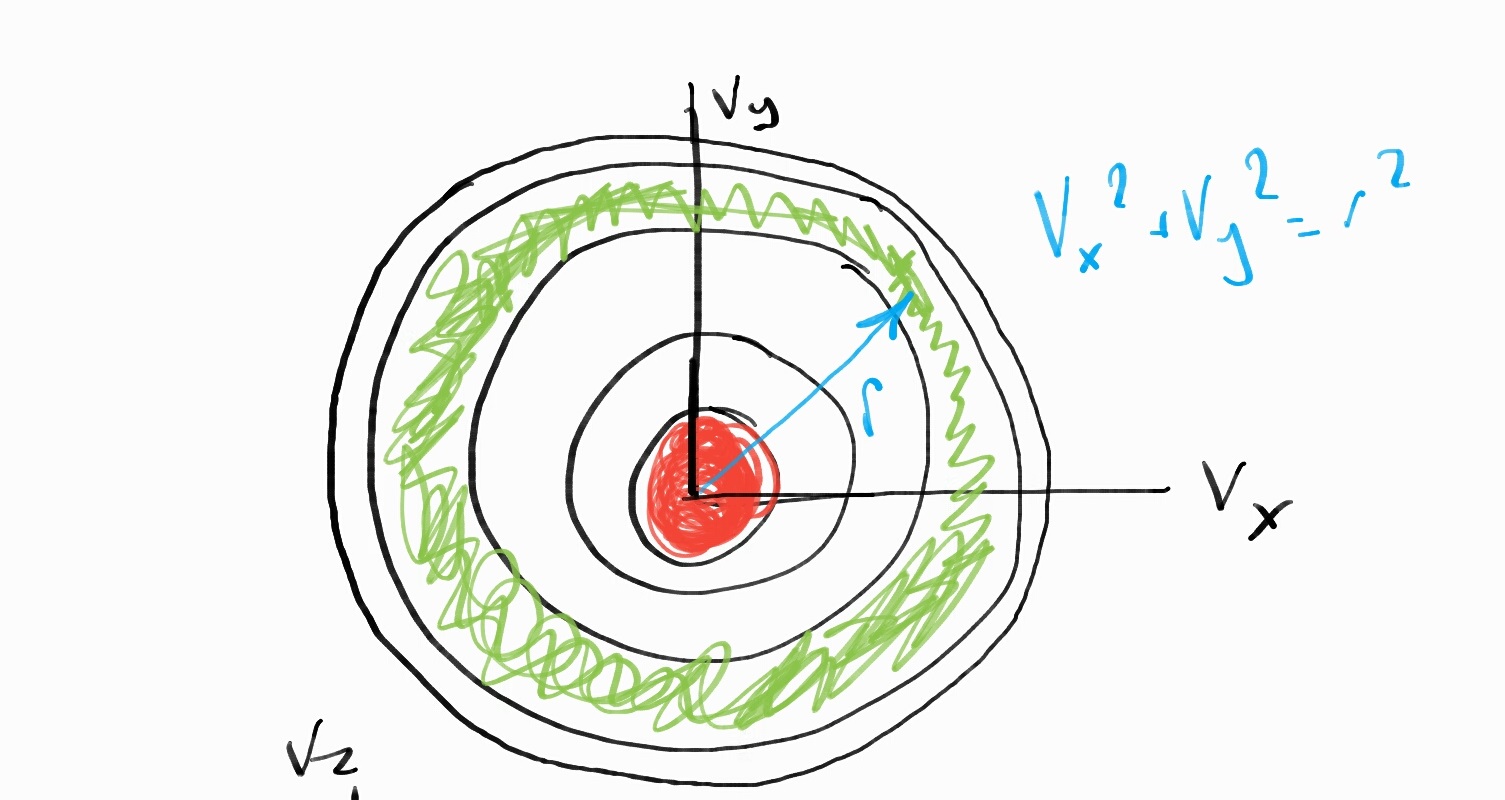
2D View of Velocity Distribution Shell
Velocity Distribution Function
This is where the Maxwellian distribution will come into play. In a real system we know that a molecule will not maintain constant velocity over time. There’s van der Waal’s forces, ionic, covalent, and metallic interactions, collisions, and a whole host of other things that can interact with the molecule. Since the main focus is rarified gas or a dilute gas we can assume intermolecular forces are negligible, (equilibrium kinetic theory).
The velocity distribution function for gas molecules in thermal equilibrium is based on symmetry. One molecule loses 5 m/s, another gains 5 m/s.
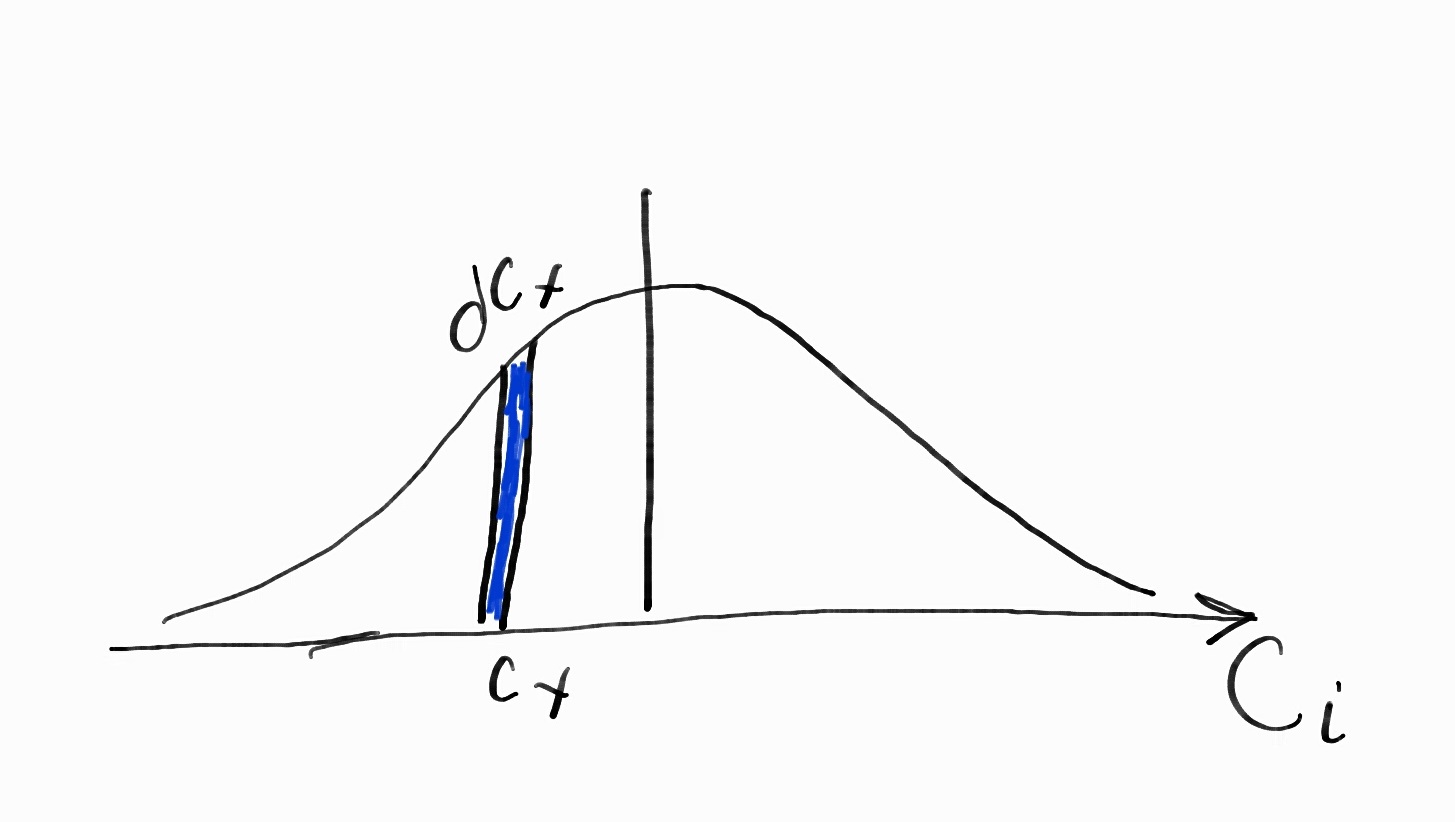
Maxwellian Distribution of Velocity
Average Quantity, Q
With N, the total number of molecules, and f(Ci), the velocity distribution we can find the average quantity. We find N from integrating the number of molecules with Ci velocity.
This average quantity can be use for anything that uses velocity: start thinking about momentum.
Some things to remember from our assumptions with equilibrium kinetic theory:
- Intermolecular forces negligible
- Collisions occur in a unit area
- All momentum is transferred through the collision process
So we could find normal stress, σ, pressure, P, or etc…
Maxwellian Distribution
Neglecting the derivation we are led to the Maxwellian distribution so that we don’t have to plot every single molecule. The Maxwellian distribution will give the probability that a molecule has speed a certain range of speed.
The information gained from using a Maxwellian distribution:
- The most probable speed of the molecules present
- The average speed of the molecules present
- The root mean square speed, Vrms
- Equation of state for perfect gas
Acknowledgements
Thanks to Dr. Wang for teaching Physical Gas Dynamics, where my notes from that class have served as the outline for this article.
I have provided links throughout this article specifically avoiding Wikipedia to help give you more references. Please credit your sources if you use them in your writing. (MLA) (AIAA)






